9th February 2021, 1 min read

Poisson Log-Normal Distributed Random Numbers

Original post is here eklausmeier.goip.de/blog/2021/02-09-poisson-log-normal-distributed-random-numbers.

Task at hand: Generate random numbers which follow a lognormal distribution, but this drawing is governed by a Poisson distribution. I.e., the Poisson distribution governs how many lognormal random values are drawn. Input to the program are $λ$ of the Poisson distribution, modal value and either 95% or 99% percentile of the lognormal distribution.

From Wikipedia's entry on Log-normal distribution we find the formula for the quantile $q$ for the $p$ -percentage of the percentile $(0 < p < 1)$ , given mean $μ$ and standard deviation $σ$ :

q = \exp (μ + \sqrt{2} σ {erf}^{- 1} (2 p - 1))

and the modal value $m$ as

m = \exp (μ - σ^{2}) .

So if $q$ and $m$ are given, we can compute $μ$ and $σ$ :

μ = \log m + σ^{2},

and $σ$ is the solution of the quadratic equation:

\log q = \log m + σ^{2} + \sqrt{2} σ {erf}^{- 1} (2 p - 1),

hence

σ_{1 / 2} = - \frac{\sqrt{2}}{2} {erf}^{- 1} (2 p - 1) \pm \sqrt{\frac{1}{2} {({erf}^{- 1} (2 p - 1))}^{2} - \log (m / q)},

or more simple

σ_{1 / 2} = - R / 2 \pm \sqrt{R^{2} / 4 - \log (m / q)},

with

R = \sqrt{2} {erf}^{- 1} (2 p - 1) .

For quantiles 95% and 99% one gets $R$ as 1.64485362695147 and 2.32634787404084 respectively. For computing the inverse error function I used erfinv.c from lakshayg.

Actual generation of random numbers according Poisson- and lognormal-distribution is done using GSL. My program is here: gslSoris.c.

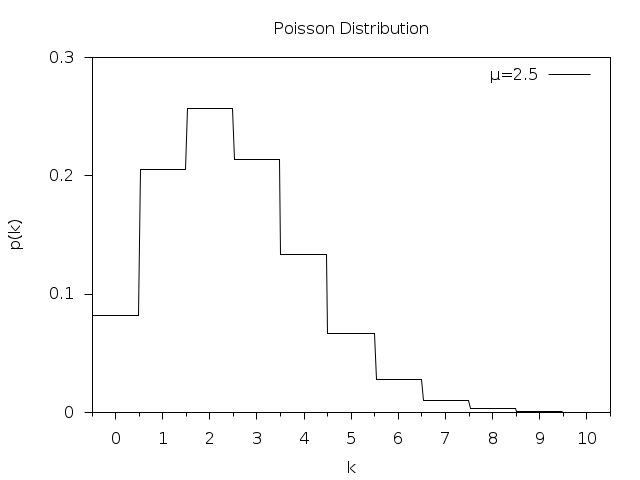
Poisson distribution looks like this (from GSL documentation):

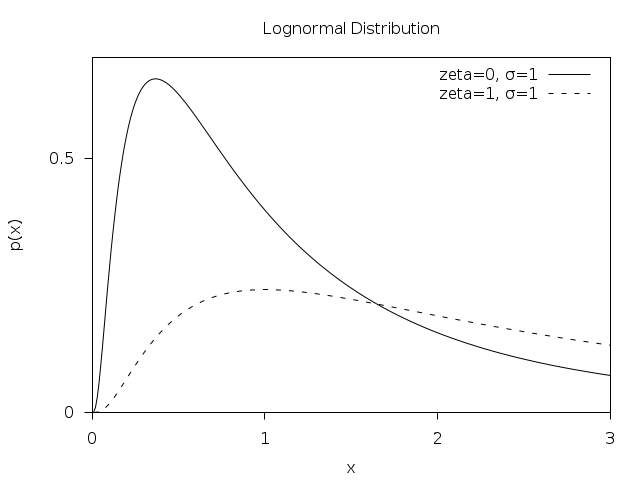
Lognormal distribution looks like this (from GSL):